الگوریتم CORDIC
فهرست مطالب:
- مقدمه
- تاریخچه
- روابط و توابع مثلثاتی
- دایره مثلثاتی
- نسبت های مثلثاتی در دایره مثلثاتی
- فیثاغورس در دایره مثلثاتی
- معرفی الگوریتم CORDIC
- مبانی الگوریتم CORDIC
- الگوریتم CORDIC
- مثال عددی الگوریتم CORDIC
مقدمه
در این مقاله به بررسی یک الگوریتم معروف در حوزه محاسبات مثلثاتی به نام CORDIC در طراحی FPGA می پردازیم.
این الگوریتم، برای محاسبه توابع مثلثاتی از جمله سینوس و کسینوس، در محیط هایی که عملیات های حسابی سخت و زمان بر هستند مورد استفاده قرار می گیرد.
همانطور که می دانیم توابع مثلثاتی یکی از مهمترین توابع در ریاضیات می باشد چرا که در بسیاری از مسائل علمی و صنعتی بطور چشمگیری مورد استفاده قرار می گیرد از کاربرد های مهم آن می توان به صنایع هوا و فضا، مسائل نظامی، ساختمان سازی، خودرو سازی و غیره اشاره نمود، در بعضی از صنایع مانند هوا فضا و محاسبات مربوط به آن سرعت پردازش اطلاعات بسیار مهم و چالش برانگیز می باشد، تصور نمایید سفینه فضایی ماهواره بر در حال پرتاب به فضا می باشد و می بایست با سرعت و مدار مشخصی از زمین ماهواره را رها نماید تا در مدار پیش بینی شده خودش قرار بگیرد، در این مسئله پردازنده ها می بایست محاسبات ریاضی و توابع مثلثاتی را به دقت بالا و در لحظه پردازش نمایند کوچکترین تاخیری موجب از دست رفتن ماهواره گران قیمت خواهد شد.
با توجه به مثال بالا می دانیم که می توان توابع مثلثاتی را با استفاده از زبان های برنامه نویسی پیاده سازی و اجرا نماییم اما اجرای این توابع بصورت نرم افزاری نیازمند زمان پردازشی زیادی است و چنانچه بخواهیم این زمان را کاهش دهیم در خصوص مثال فوق نیاز به منابع سخت افزاری سریعتری خواهیم داشت، که این یعنی افزایش وزن و افزایش مصرف انرژی، اگر بتوانیم الگوریتم های مهم و پر کاربرد را بصورت مدارات سخت افزاری پیاده سازی نماییم در این صورت توانسته ایم بدون افزایش چشمگیر منابع سخت افزاری و مصرف انرژی زمان پردازش را کاهش داده و نتیجه مطلوب را کسب نماییم.
با استفاده از الگوریتم CORDIC می توانیم سرعت محاسبات توابع مثلثاتی را بطور چشمگیر و فزاینده ای افزایش دهیم و از طرف دیگر می توانیم این الگوریتم را بصورت سخت افزاری پیاده سازی نماییم که این روش می تواند بطور چشمگیری ما را به اهداف تعیین شده مثال فوق برساند.
الگوریتم CORDIC ، نسخه ساده الگوریتم چرخشی است که در سال 1959 توسط جان وولف کاندل (John Wallis Kendl) ابداع شده است، نام CORDIC به معنای “محاسبه ی موقعیت دایره ای در دستگاه مختصات” است، این الگوریتم بسیار سریع و دقیق است و می تواند در محاسبات واقعی زمان بر مورد استفاده قرار گیرد.
در ادامه پس بررسی مختصری از تاریخچه الگوریتم فوق و برای درک بهتر آن، ابتدا مروری بر روابط مثلثاتی و فرمول های آن خواهیم داشت.
تاریخچه
در سال ۱۹۵۹، جان ولدر (John Volder)، مهندس برق آمریکایی، یک الگوریتم جدید برای محاسبات روابط مثلثاتی ابداع کرد، این الگوریتم با نام Volder’s Algorithm شناخته می‌شود و از تکنیک هایی مبتنی بر جمع و تفریق چند جمله ای استفاده می کرد.
همچنین در سال ۱۹۶۰، ویلیام کارلسون (William Kahan)، ریاضی دان و مهندس برق، با نام گذاری الگوریتم CORDIC، این الگوریتم را بهبود داد. نام CORDIC مخفف عبارت Coordinate Rotation Digital Computer می باشد و به توصیف روش الگوریتم اشاره دارد.
از آن زمان به بعد، الگوریتم CORDIC به عنوان یک روش معمول برای محاسبات روابط مثلثاتی در دستگاه های دیجیتالی و کامپیوترها مورد استفاده قرار گرفته است.
روابط و توابع مثلثاتی
مثلثات یکی از مهمترین مسائل مباحث ریاضیات محسوب می شود که بررسی روابط میان طول اضلاع و زاویه های مثلث می پردازد، این شاخه از ریاضیات کاربردهای بسیار متنوعی دارد که از جمله آن می توان به مطالعات اخترشناسی، فیزیک، ریاضی محض، و ریاضیات مهندسی اشاره کرد، بسیاری از روش های بنیادی تحلیلی مانند تبدیل فوریه و معادلات موج اشاره نمود، شایان ذکر است که اولین بار دانشمند توانا و بنام کشور عزیزمان خواجه نصیرالدین طوسی، مثلثات را بعنوان شاخه ای از ریاضیات به جوامع علمی معرفی نمود وی همچنین مثلثات کروی را به شکل امروزی آن بیان کرد.
می دانیم که در هندسه با استفاده از دو نقطه می توانیم خطوط را ترسیم نماییم و همچنین می دانیم با استفاده از خطوط می توانیم اشکال هندسی را ترسیم نماییم، که مثلث نیز از به هم پیوستن سه پاره خط تشکیل شده است که آن نیز انواع مختلفی دارد.
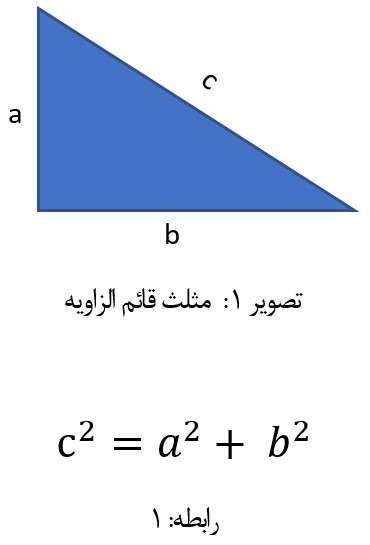
در خصوص روابط مثلثاتی، شکل هندسی مثلث قائم الزاویه مورد نظر می باشد چرا که این مثلث از آن نظر حائز اهمیت است که از آن برای تعریف روابط مهم و پایه ای مثلثات استفاده می شود و از طرف دیگر قضیه فیثاغورس در مورد اضلاع آن صادق و جاری می باشد.
در ادامه برای درک بهتر و روشن تر از موضوع، مطالب را با بررسی یک مثلث قائم الزاویه ادامه می دهیم.
در یک مثلث قائم الزاویه، ضلعی که روبروی زاویه عمود قرار گرفته است را وتر می نامیم، همچنین می دانیم، وتر از دو ضلع دیگر بزرگتر است.
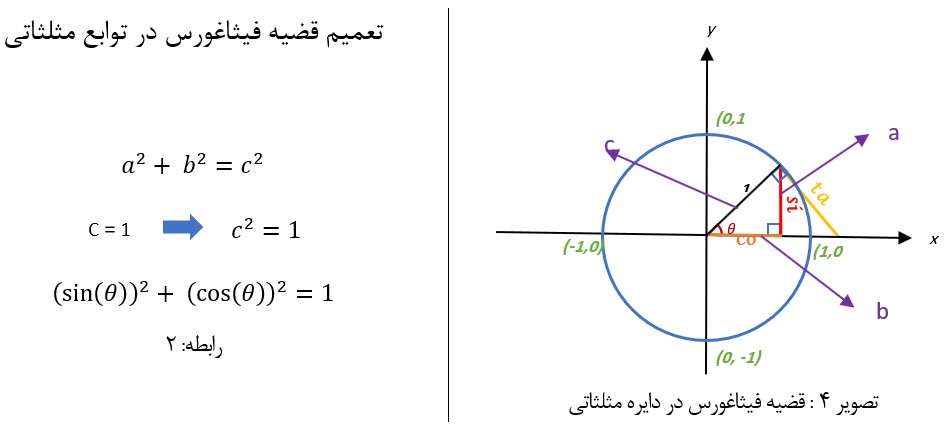
بر این اساس مطابق تصویر: 1، اگر اضلاع مثلث قائم الزاویه را به ترتیب a, b, c نام گذاری کنیم بطوری که c وتر آن باشد، رابطه فیثاغورس در مورد آن بشرح ذیل می باشد:
بر اساس قانون و یا قضیه فیثاغورس و تعمیم آن به روابط مثلثاتی خواهیم رسید که در ادامه به آن می پردازیم.
دایره مثلثاتی
برای آشنایی بیشتر با روابط مثلثاتی ابتدا باید به مطالعه دایره مثلثاتی بپردازیم، باید متذکر شویم که این دایره بگونه ای خاص است، چرا که شعاع آن را یک واحد در نظر گرفته اند، یعنی می توان یک میلی متر، یک سانتی متر و یا هر واحد دیگری برای آن در نظر گرفت ولی مهم این است که این اندازه مبنی و معیار اصلی ما می باشد و بر اساس آن اندازه های دیگر را می توان محاسبه نمود چرا که نسبت های مثلثاتی به صورت کسری از اضلاع مثلث درون این دایره می باشند بنابراین واحد اندازه گیری آن مد نظر نمی باشد چرا که با استفاده از تناسب می توانیم سایر واحد را محاسبه نماییم، لذا با بزرگ و کوچک شدن دایره یعنی تغییر شعاع آن نسبت ها تغییر نکرده و برای زاویه های یکسان ثابت و برابر هستند، از همین روی می توان به عدد π را اشاره نمود که نسبت محیط به قطر دایره می باشد و همواره مقداری بدون واحد است.
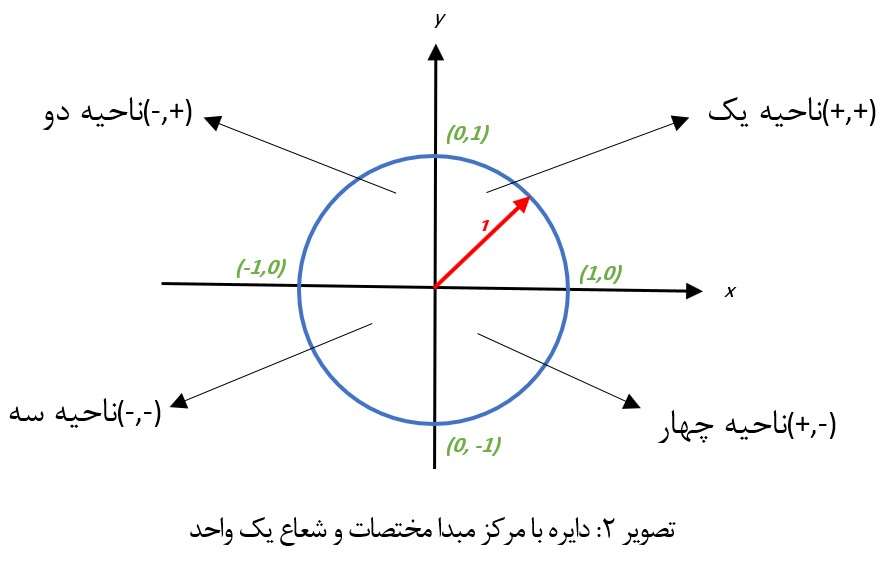
در تصویر:2، یک دایره با شعاع واحد که مرکز آن در مبدا مختصات دکارتی منطبق شده است قابل مشاهده می باشد، محور های x, y دایره فوق را به چهار ناحیه متفاوت ولی با اندازه های یکسان تقسیم کرده اند، به مختصات برخورد دایره با محور ها در هر ناحیه توجه نمایید، محل برخورد دایره با محور افقی x در ناحیه مثبت محور در نقطه (1,0) و در ناحیه منفی محور در نقطه (-1,0) می باشد، همچنین محل برخورد دایره با محور عمودی y در ناحیه مثبت محور در نقطه (0,1) و در ناحیه منفی محور در نقطه (0,-1) می باشد.
همانطور که در تصویر 2 قابل مشاهده است محور دایره مثلثاتی را به چهار ناحیه مجزا تقسیم کرده است، لذا به این نواحی اصطلاحا ربع دایره مثلثاتی نیز گفته می شود، لذا می توان از اصطلاح ربع اول تا چهارم برای مشخص نمودن این نواحی نیز استفاده نمود.
نسبت های مثلثاتی در دایره مثلثاتی
بطور مثال یک نقطه را روی دایره مثلثاتی مطابق تصویر: 3، در نظر بگیرید، در ادامه از آن نقطه خطی عمود بر محور افقی یا x ایجاد نمایید، پس از آن از مبدا مختصات شعاع دایره را طوری رسم کنید که بر نقطه ای که روی دایره در نظر گرفته بودید منتهی شود، در نهایت شما یک مثلث قائم زاویه را می توانید پس از ترسیم خطوط فوق در داخل دایره مثلثاتی مشاهده نمایید، برای درک بهتر مسئله به تصویر: 3 توجه نمایید:
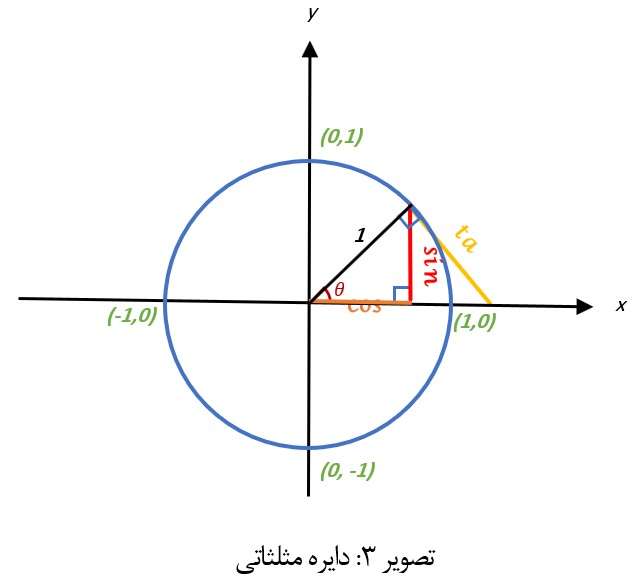
همانطور که در تصویر فوق قابل مشاهده است مثلث مذکور دارای قاعده ای است که مماس بر محور افقی x می باشد و در طرف دیگر ارتفاع مثلث است که خطی موازی با محور عمودی y می باشد، همچنین وتر مثلث مذکور، در واقع شعاع دایره مثلثاتی است، حال اگر نقطه ابتدایی تصور ما یعنی انتهای پاره خط وتر مثلث، بر روی دایره جابجا شود اندازه دو ضلع دیگر مثلث یعنی ارتفاع و قاعده آن نیز تغییر خواهد کرد، آنچه که مسلم است به هیچ عنوان اندازه وتر مثلث تغییر نخواهد داشت، چرا که وتر مثلث مذکور شعاع دایره مثلثاتی است و همواره یک واحد می باشد، در ادامه اگر انتهای وتر حول نقطه مرکز مختصات چرخش دهیم مثلا آن را به محور افقی نزدیک نماییم متوجه می شویم اندازه ضلع قاعده مثلث افزایش پیدا می کند تا جایی که اگر وتر را بر محور افقی مماس کنیم اندازه قاعده برابر با شعاع خواهد شد در حالی که اندازه ضلع ارتفاع بسیار کوچک و در حالت وتر مماس به محور افقی برابر صفر خواهد شد، در نقطه مقابل اگر وتر مثلث را به محور عمودی نزدیک نماییم اندازه ضلع ارتفاع برابر شعاع خواهد شد و ضلع قاعده برابر صفر خواهد شد، از این توضیح می توان متوجه شد که این تغییرات رابطه مستقیمی به تغییر زاویه وتر با قاعده دارد که در تصویر:3 نام آن زاویه θ (تِتا) نهاده شده است، در نتیجه می توان بر اساس زاویه θ اندازه هر ضلع مثلث با وتری به شعاع یک واحد را محاسبه نمود، از توضیحات فوق و بنا به تعریف ریاضی آن به ضلع قاعده مثلث تصویر: 3 ،کسینوس زاویه تتا و به ضلع ارتفاع آن سینوس می گویند، همچنین متوجه شدیم که کسینوس زاویه صفر درجه برابر یک و سینوس آن برابر با صفر می باشد، در نقطه مقابل سینوس زاویه 90 درجه برابر یک و کسینوس آن برابر صفر خواهد شد.
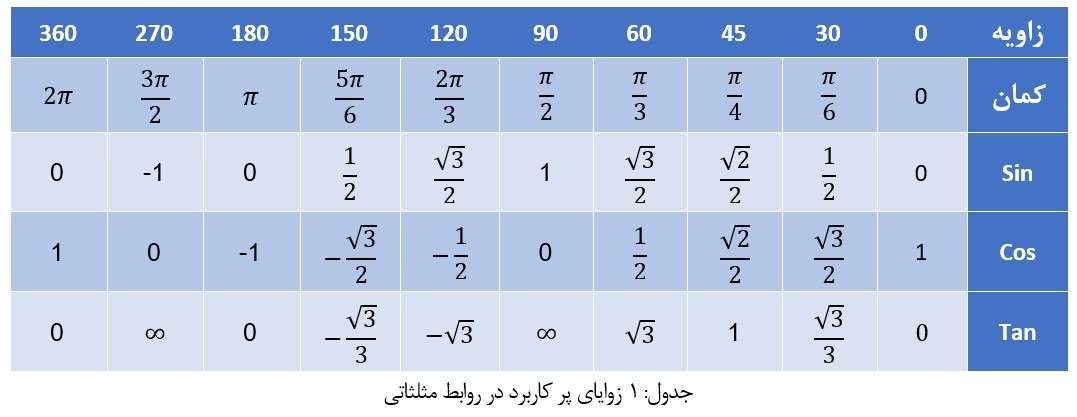
در جدول ذیل زوایای مهم و نسبت مثلثاتی آن به منظور مطالعه بیشتر آماده شده است.
فیثاغورس در دایره مثلثاتی
همانطور که قبلا اشاره شد طبق قضیه فیثاغورس مجموع مربع دو ساق مثلث برابر با مربع وتر می باشد، بر همین اساس می توان مطابق شکل 4 روابط زیر را به قضیه فیثاغورس تعمیم داد.
در ادامه نیز می توان بر اساس رابطه: 2 روابط زیر را نتیجه گرفت:
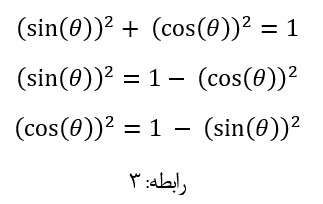
معرفی الگوریتم CORDIC
CORDIC مخفف عبارت Coordinate Rotation Digital Computer می باشد، که الگوریتمی بسیار بهینه و مناسب برای پیاده سازی محاسبه توابع مثلثاتی در محیط های سخت افزاری با دقت بسیار بالا می باشد، که به آن اصطلاحا Hardware Efficient می گویند.
می دانیم در مسائلی نیاز به محاسبات مثلثاتی و یا توابع لگاریتمی داریم مانند پروژه هایی که محاسبات مختصات بردار ها در آن ها بکار می رود، در زبان های برنامه نویسی با استفاده از کتابخانه ها و توابع مثلثاتی می توانیم محاسبات لازم را انجام داده و از حاصل نتایج آن بهرمند گردیم، اما در برخی موارد به علت محدودیت های موضوع پروژه که در بیشتر موارد سرعت محاسبات می باشد نمی توانیم محاسبات را بصورت نرم افزاری انجام دهیم چرا که بعضا نیاز به پردازش های Real Time می باشد و همچنین می دانیم اجرای نرم افزار ها به عوامل متعددی بستگی دارد که از جمله آن می توان به موارد ذیل اشاره نمود:
- معماری پردازنده
- فضای آدرس دهی
- سرعت Fetch و Execute فرامین
- مقدار مصرف توان
- تولید گرما
- هزینه های ساخت
از همین روی می توانیم با یک طراحی کارآمد، محاسبات فوق را بصورت سخت افزاری انجام دهیم، پردازش های سخت افزاری بطرز بسیار چشمگیری می تواند زمان اجرای محاسبات را کاهش دهد و از طرف دیگر بسیاری از مشکلات پردازش های نرم افزاری که به آن اشاره کردیم را در پی نخواهد داشت.
توجه داشته باشید برای محاسبه و پیاده سازی توابع مثلثاتی بصورت سخت افزاری روش های متعددی موجود است، که از جمله آن ها می توان به استفاده از سری های توانی و بسط تیلور اشاره نمود، اما در همه این موارد ما به مکانیزم های ضرب کننده نیاز داریم، در مقابل آن برای نیل رسیدن به اهدافی مانند کاستن از پیچیدگی، سهولت در پیاده سازی، مصرف توان اندک و بسیاری از موارد دیگر می توان به الگوریتم CORDIC اشاره نمود که از منظر های بسیاری بهینه و پر کاربرد می باشد.
با استفاده از الگوریتم فوق می توانیم توابع معکوس مثلثاتی مانند:
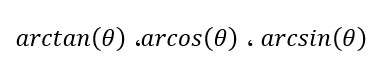
همچنین توابع هایپربولیک و لگاریتمی را نیز محاسبه نماییم، علاوه بر آن نیز می توانیم با استفاده از این الگوریتم تبدیل نقاط در دستگاه های مختلف مختصاتی مانند کارتزین به قطبی و برعکس را نیز محاسبه نماییم.
مبانی الگوریتم CORDIC
این الگوریتم برای محاسبه توابع مثلثاتی به این صورت عمل می کند که ابتدا برداری را در نقطه
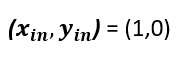
در نظر می گیرد زاویه مورد نظر را به عنوان ورودی دریافت کرده، حال بردار فوق را در جهت رسیدن به زاویه ورودی دَوَران (چرخش) می دهد، با چرخش و دَوَران پاره خط در دایره مثلثاتی حول نقطه مرکز مختصات زاویه ای بدست می آید که نام آن را تتا می نهیم، حال می دانیم طبق روابط مثلثاتی می توانیم با داشتن زاویه تتا مختصات جدید نقاط
را محاسبه نماییم، در ادامه روابطی را که می توان برای محاسبه دوران و چرخش مورد استفاده قرار گیرند مورد بررسی قرار خواهیم داد، اما قبل از آن برای درک بهتر موضوع به تصویر 6 توجه نمایید.
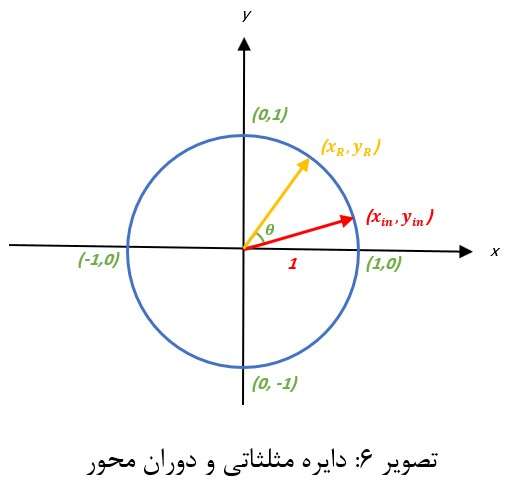
همانطور که اشاره شد مطابق تصویر 6 فرض کنید سیستمی قادر است یک بردار را مانند:
دریافت کرده و آن را مطابق یک زاویه انتخابی مانند تتا دوران (چرخش) دهد که در نتیجه آن بردار:
حاصل می شود، با توجه به روابط مثلثاتی و توابع دوران و چرخش می توان بر اساس زاویه چرخش مختصات نقاط
را از طریق رابطه: 4 محاسبه نمود که بدین بشرح می باشد:
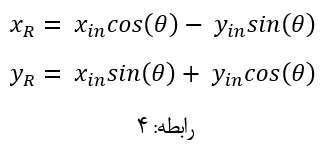
حال که متوجه شدیم می توان با داشتن مختصات یک نقطه به عنوان مبدا دوران و همچنین زاویه دوران مختصات نقاط جدید را محاسبه نمود، می خواهیم مسئله فوق را ساده سازی نماییم و فرض مسئله را طوری بیان نماییم که بخشی از معادله ساده سازی شود، از همین روی مجددا یک دایره مثلثاتی با شعاع یک واحد را فرض خواهیم کرد، همچنین مختصات بردار اولیه را یعنی:
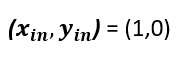
در نظر خواهیم گرفت، درادامه برای درک بهتر موضوع به تصویر 7 را مورد توجه قرار دهید:
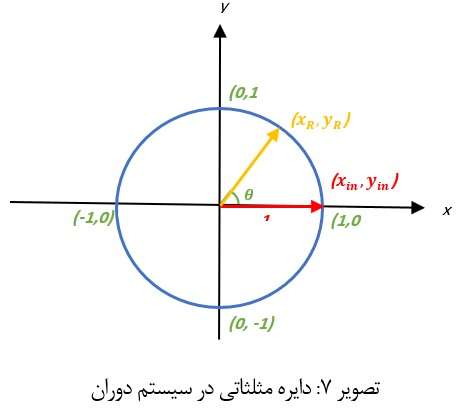
همانطور که اشاره شد بر اساس تصویر 7 چنانچه مختصات اولیه بردار
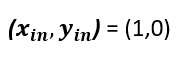
باشد و بردار مورد نظر به اندازه زاویه تتا دوران نماید، بر اساس مختصات فوق و رابطه: 4 خواهیم داشت:
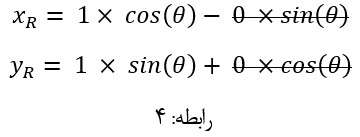
پس از ساده سازی و ضرب متغیر ها، طبق رابطه فوق مختصات نقاط
برابر با مقادیر ذیل خواهد شد:
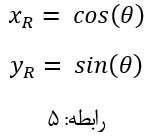
با کمی دقت و بررسی روابط فوق خواهیم دریافت که در دایره مثلثاتی مفروض مسئله یاد شده، نسبت های مثلثاتی را می توان از طریق مختصات های جدید نیز بدست آورد، به بیان دیگر طبق این تعریف می توانیم بجای اینکه از طریق روابط دوران به مختصات جدید دست یابیم می توانیم با داشتن مختصات بردار مبدا و بردار مقصد توابع مثلثاتی را محاسبه نماییم به عبارتی دیگر:
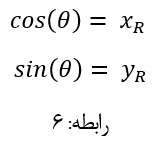
از روابط فوق می توان اینطور برداشت کرد که برای محاسبه
را تا جایی دوران دهیم که به زاویه مورد نظرمان برسد، پس از آن بر اساس نقاط مختصات بدست آمده جدید و از طریق رابطه 6 می توان مقدار دقیق سینوس و کسینوس تتا را بدست آوریم، توضیح فوق دقیقا اساس و منطق الگوریتم CORDIC می باشد.
الگوریتم CORDIC
همانطور که در مبانی الگوریتم CORDIC اشاره شد، می توان با دوران بردار
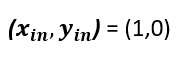
حول مبدا مختصات به اندازه زاویه مورد نظرمان یعنی تتا می توانیم از طریق رابطه 6 مقادیر توابع کسینوس تتا و سینوس تتا را محاسبه نماییم، اما برای این منظور می بایست دوران را حول مبدا مختصات را بصورت مرحله به مرحله انجام دهیم، یعنی زاویه مورد نظرمان را تقسیم بندی نماییم و هر مرحله یک دوران را انجام دهیم، مختصات جدید نقاط
را بدست آورده و مجددا در مرحله بعد مختصات بدست آمده را بعنوان مبدا در نظر گرفته و دوران را ادامه دهیم، این مراحل تا جایی ادامه می یابد که به زاویه مورد نظر مان برسیم، اما قبل از آن باید به خاطر بیاوریم که قرار است همه این مراحل در سخت افزار انجام شود و اگر قرار باشد محاسبات در مبنایی به غیر از باینری انجام گردد مجددا در چالش محاسبات پیچیده و مشکلات مربوط به آن که در قسمت های قبل توضیح داده شد قرار خواهیم گرفت، لذا می بایست برای رهایی از این مشکل بدنبال راه حلی مناسب و کارآمد باشیم، خوشبختانه الگوریتم CORDIC راه حل بسیار جالبی ارائه کرده است که بسادگی می توان محاسبات را در مبنی باینری انجام داد که در ادامه به بررسی آن خواهیم پرداخت، اما قبل از آن برای درک بهتر و روشن تر شدن موضوع بهتر است جدول 2 را مورد بررسی قرار داده تا بتوان جزئیات ارائه شده در الگوریتم CORDIC را مورد مطالعه قرار دهیم.
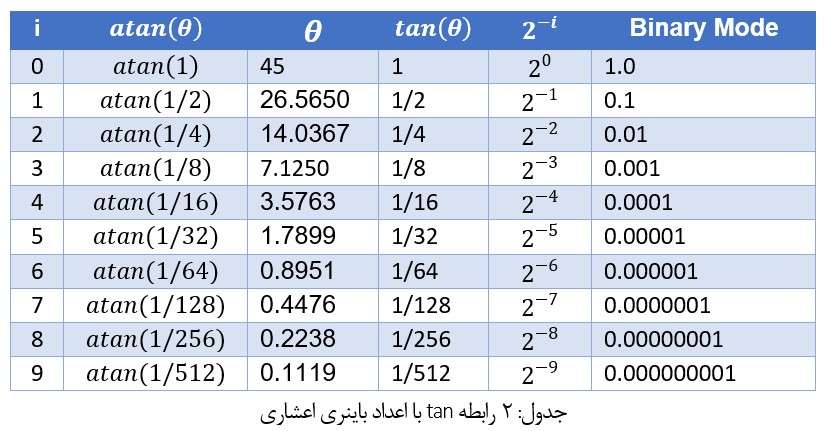
در جدول 2 نشان داده شده است که اعداد شناور باینری (اعشاری) رابطه مستقیمی با تانژانت زوایای مشخصی دارد (جدول 2 ستون زاویه تتا) لذا اگر بتوانیم روابط 5 و 6 را بگونه ای تغییر دهیم که بجای استفاده از توابع سینوس تتا و سینوس تتا از تانژانت تتا استفاده نماییم می توانیم به هدف مان که پیاده سازی توابع مثلثاتی در سخت افزار است نزدیکتر شویم، خوشبختانه طبق روابط مثلثاتی می دانیم که:
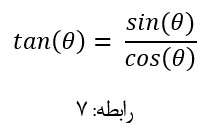
بر همین اساس می توان روابط را بدین گونه بازنویسی کرد:
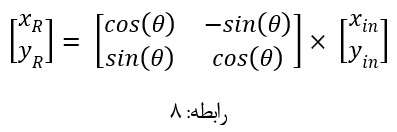
با توجه به رابطه: 7 می توان درایه های ماتریس چهار در چهار داخلی رابطه: 8 را بر کسینوس تتا تقسیم نمود به رابطه ذیل تبدیل نمود:
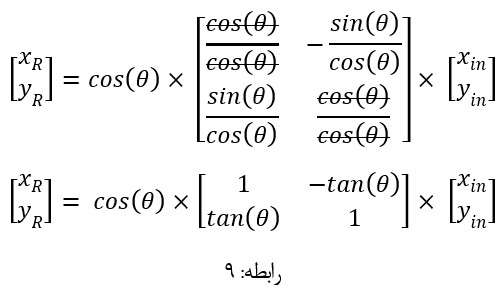
حال با داشتن رابطه 9 می توانیم براحتی محاسبات را در سخت افزار پیاده سازی نماییم چرا که می دانیم:
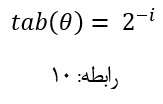اما همچنان چند نکته از محاسبات باقی مانده است که در ادامه به بررسی راه حل های ارائه شده می پردازیم.
بر طبق الگوریتم CORDIC ما بردار مبدا را حول نقطه مبدا متخصات بر اساس زوایای قرینه تانژانت تتا تا جایی دوران می دهیم که به زاویه صفر درجه برسیم یعنی زوایای جدول 2 را از زاویه مد نظرمان تفریق می کنیم لذا بدلیل اینکه زوایای ما از 45 درجه شروع می شود و در هر مرحله اعداد زاویه های جدول 2 با مقادیر مختلفی از زاویه مد نظر ما کسر می شود، ممکن است جهت محاسبات تغییر کند برای جلوگیری از این موضوع از یک متغییر تغییر علامت در محاسبات استفاده خواهیم نمود که به اختصار نام آن را d که مخفف Direction است، می گذاریم، هر بار که زاویه مد نظر ما از زاویه جدول 2 کسر بیت علامت حاصل باقی مانده را بررسی می نماییم چنانچه منفی باشد d را برابر -1 و در غیر این صورت d = 1 خواهد شد حال با این توضیح و با توجه به رابطه های 9 و 10 ، فرمول نهایی الگوریتم CORDIC بشرح ذیل می باشد:
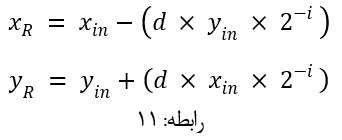
همچنان یک نکته دیگر باقی مانده است که آن هم ضریب کسینوس تتا در رابطه 9 می باشد از آنجایی که طبق جدول 2 زاویه تتا در هر مرحله به سمت صفر میل می نماید بنابر این طی 6 مرحله محاسبات کسینوس تتا مطابق رابطه زیر عددی ثابت خواهد شد:
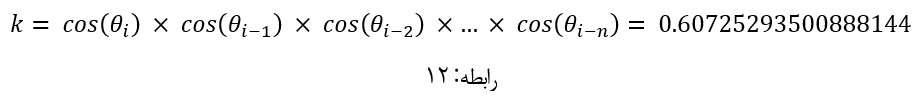
لذا می توان ثابت K را بعنوان مبدا بردار یعنی در نظر گرفت با این روش دیگر نیازی هم به مدار ضرب کننده نمی باشد، همچنین می توانیم مقادیر ثابت زاویه های جدول 2 را در حافظه ROM سخت افزار ذخیره نماییم و با استفاده از آن در مرحله عملیات جمع یا تفریق را در سیستم انجام دهیم.
حال که با الگوریتم CORDIC بطور کامل آشنا شدیم، سعی خواهیم کرد الگوریتم فوق را با یک مثال عددی مورد بررسی قرار دهیم.
مثال عددی الگوریتم CORDIC
فرض کنید زاویه مد نظر ما برابر با Z = 10 درجه می باشد بر همین اساس می توانیم مقادیر کسینوس تتا و سینوس تتا را با دوران بردار فوق طی چند مرحله محاسبه نماییم هر چه تعداد مراحل بیشتر باشد دقت محاسبات نیز بیشتر خواهد بود که این امر تاثیر بسزایی در مساحت سخت افزار و زمان اجرا خواهد داشت یادآور می شود در مثال فوق برای درک بهتر اعداد باینری بیت علامت را صرفه نظر کرده و مستقیم علامت منفی لحاظ شده است:
Sin: 0.173648177
Cos: 0.984807753
First Start:
x: 0.607252935008881 Binary Values: 0.10011011011101001110110110101000010000110101111001101
y: 0 Binary Values: 0.
z: 10 Binary Values: 1010.
——————————————–
Loop No:0
x: 0.607252935008881 Binary Values: 0.10011011011101001110110110101000010000110101111001101
y: 0 Binary Values: 0.
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.607252935008881 Binary Values: 0.10011011011101001110110110101000010000110101111001101
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.607252935008881 Binary Values: 0.10011011011101001110110110101000010000110101111001101
z – (d * angles[0]): 10 – (1 * 45) = -35 Binary Values: -100010.11111111111111111111111111111111111111111111101
d: 1
——————————————–
Loop No:1
x: 0.607252935008881 Binary Values: 0.10011011011101001110110110101000010000110101111001101
y: 0.607252935008881 Binary Values: 0.10011011011101001110110110101000010000110101111001101
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.910879402513322 Binary Values: 0.111010010010111101100100011111000110010100001101101
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.303626467504441 Binary Values: 0.010011011011101001110110110101000010000110101111001101
z – (d * angles[1]): -35 – (-1 * 26.565051177078) = -8.434948822922 Binary Values: -1000.011011110101100011001110010110011110001000111
d: -1
——————————————–
Loop No:2
x: 0.910879402513322 Binary Values: 0.111010010010111101100100011111000110010100001101101
y: 0.303626467504441 Binary Values: 0.010011011011101001110110110101000010000110101111001101
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.986786019389432 Binary Values: 0.1111110010011110000000100011000101101101011110010111
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.0759066168761102 Binary Values: 0.000100110110111010011101101101010000100001101011110011
z – (d * angles[2]): -8.434948822922 – (-1 * 14.0362434679265) = 5.60129464500447 Binary Values: 101.1001100111101110011100100010001110001101110111001
d: -1
——————————————–
Loop No:3
x: 0.986786019389432 Binary Values: 0.1111110010011110000000100011000101101101011110010111
y: 0.0759066168761102 Binary Values: 0.000100110110111010011101101101010000100001101011110011
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.977297692279919 Binary Values: 0.11111010001100000010111001111010110011000110101111111
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.199254869299789 Binary Values: 0.0011001100000010010111011111101100110110000110101111101
z – (d * angles[3]): 5.60129464500447 – (1 * 7.12501634890177) = -1.5237217038973 Binary Values: -1.10000110000100101010000000100110011100011011110101
d: 1
——————————————–
Loop No:4
x: 0.977297692279919 Binary Values: 0.11111010001100000010111001111010110011000110101111111
y: 0.199254869299789 Binary Values: 0.0011001100000010010111011111101100110110000110101111101
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.989751121611156 Binary Values: 0.11111101011000000101010001011010011111111100110110101
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.138173763532294 Binary Values: 0.0010001101011111010110110001001110001001010101000011101
z – (d * angles[4]): -1.5237217038973 – (-1 * 3.57633437499735) = 2.05261267110005 Binary Values: 10.000011010111100000000110001001011011101011011011111
d: -1
——————————————–
Loop No:5
x: 0.989751121611156 Binary Values: 0.11111101011000000101010001011010011111111100110110101
y: 0.138173763532294 Binary Values: 0.0010001101011111010110110001001110001001010101000011101
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.985433191500771 Binary Values: 0.11111100010001010101100110000001111000111000001100001
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.169103486082643 Binary Values: 0.00101011010010100101110110110110010111010101001010101
z – (d * angles[5]): 2.05261267110005 – (1 * 1.78991060824606) = 0.262702062853985 Binary Values: 0.010000110100000001110001010000001000110010110010100111
d: 1
——————————————–
Loop No:6
x: 0.985433191500771 Binary Values: 0.11111100010001010101100110000001111000111000001100001
y: 0.169103486082643 Binary Values: 0.00101011010010100101110110110110010111010101001010101
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.98279094953073 Binary Values: 0.11111011100110000011000000001011000010100000110111
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.184500879699842 Binary Values: 0.001011110011101101110011000111000110010011100000101101
z – (d * angles[6]): 0.262702062853985 – (1 * 0.895173710211073) = -0.632471647357088 Binary Values: -0.1010000111101001101010010111000100001011110000101001
d: 1
——————————————–
Loop No:7
x: 0.98279094953073 Binary Values: 0.11111011100110000011000000001011000010100000110111
y: 0.184500879699842 Binary Values: 0.001011110011101101110011000111000110010011100000101101
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.984232362653385 Binary Values: 0.1111101111110110101001101111000101000010110101111
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.176822825406634 Binary Values: 0.00101101010001000100001010111100010011101100110010011
z – (d * angles[7]): -0.632471647357088 – (-1 * 0.447614170860553) = -0.184857476496535 Binary Values: -0.0010111101010010110100011100111111111001010001001101
d: -1
——————————————–
Loop No:8
x: 0.984232362653385 Binary Values: 0.1111101111110110101001101111000101000010110101111
y: 0.176822825406634 Binary Values: 0.00101101010001000100001010111100010011101100110010011
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.98492307681513 Binary Values: 0.1111110000100011111010110011001111111111001001100101
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.172978167740019 Binary Values: 0.00101100010010000100110000010101010111011000100111
z – (d * angles[8]): -0.184857476496535 – (-1 * 0.223810500368538) = 0.038953023872003 Binary Values: 0.00001001111110001101001101001011100111000100110110101111
d: -1
——————————————–
Loop No:9
x: 0.98492307681513 Binary Values: 0.1111110000100011111010110011001111111111001001100101
y: 0.172978167740019 Binary Values: 0.00101100010010000100110000010101010111011000100111
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.984585228831263 Binary Values: 0.11111100000011011100011100001101111101000111011110001
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.174901845624423 Binary Values: 0.001011001100011001011110000010101111011110001001010101
z – (d * angles[9]): 0.038953023872003 – (1 * 0.111905677066206) = -0.0729526531942034 Binary Values: -0.000100101010110100000110011010111010000000100010111101
d: 1
——————————————–
Loop No:10
x: 0.984585228831263 Binary Values: 0.11111100000011011100011100001101111101000111011110001
y: 0.174901845624423 Binary Values: 0.001011001100011001011110000010101111011110001001010101
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.98475603141488 Binary Values: 0.11111100000110001111100010100101011101110011010101101
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.173940336611893 Binary Values: 0.0010110010000111010110101001100100110100000011000011011
z – (d * angles[10]): -0.0729526531942034 – (-1 * 0.0559528918938037) = -0.0169997613003997 Binary Values: -0.000001000101101000011000101010101101001100110100101101
d: -1
——————————————–
Loop No:11
x: 0.98475603141488 Binary Values: 0.11111100000110001111100010100101011101110011010101101
y: 0.173940336611893 Binary Values: 0.0010110010000111010110101001100100110100000011000011011
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.984840963219866 Binary Values: 0.11111100000111101000100110010000110010100101101111101
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.173459498705929 Binary Values: 0.0010110001100111110101110111101000011111010111010101
z – (d * angles[11]): -0.0169997613003997 – (-1 * 0.0279764526170038) = 0.0109766913166041 Binary Values: 0.00000010110011110101111001010010001110010001110100110100101
d: -1
——————————————–
Loop No:12
x: 0.984840963219866 Binary Values: 0.11111100000111101000100110010000110010100101101111101
y: 0.173459498705929 Binary Values: 0.0010110001100111110101110111101000011111010111010101
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.98479861470944 Binary Values: 0.1111110000011011110000110001001101010010101110011111
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.173699938394215 Binary Values: 0.0010110001110111100110010110001010111000011010011111011
z – (d * angles[12]): 0.0109766913166041 – (1 * 0.0139882271422649) = -0.00301153582566079 Binary Values: -0.000000001100010101011101001011111110000111000111001011010111
d: 1
——————————————–
Loop No:13
x: 0.98479861470944 Binary Values: 0.1111110000011011110000110001001101010010101110011111
y: 0.173699938394215 Binary Values: 0.0010110001110111100110010110001010111000011010011111011
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.984819818315201 Binary Values: 0.1111110000011101001001101101000000011101110011111011
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.173579723719568 Binary Values: 0.001011000110111110111000100001001001111111001111011
z – (d * angles[13]): -0.00301153582566079 – (-1 * 0.00699411367535291) = 0.00398257784969212 Binary Values: 0.000000010000010100000000100100011001111001000010011101100111
d: -1
——————————————–
Loop No:14
x: 0.984819818315201 Binary Values: 0.1111110000011101001001101101000000011101110011111011
y: 0.173579723719568 Binary Values: 0.001011000110111110111000100001001001111111001111011
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.984809223849642 Binary Values: 0.1111110000011100011101010001000100111011101111010011
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.173639832351057 Binary Values: 0.00101100011100111010100011111001001110110000111111011
z – (d * angles[14]): 0.00398257784969212 – (1 * 0.00349705685070408) = 0.000485520998988034 Binary Values: 0.00000000000111111101000110110000110011111110101010110000111111
d: 1
——————————————–
Loop No:15
x: 0.984809223849642 Binary Values: 0.1111110000011100011101010001000100111011101111010011
y: 0.173639832351057 Binary Values: 0.00101100011100111010100011111001001110110000111111011
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.984803924782493 Binary Values: 0.11111100000111000001110000101001111010011100101010111
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.173669886343484 Binary Values: 0.0010110001110101101000010011001000100101001100100101
z – (d * angles[15]): 0.000485520998988034 – (1 * 0.00174852842698067) = -0.00126300742799264 Binary Values: -0.00000000010100101100010110111111100110010000101110011101000101
d: 1
——————————————–
Loop No:16
x: 0.984803924782493 Binary Values: 0.11111100000111000001110000101001111010011100101010111
y: 0.173669886343484 Binary Values: 0.0010110001110101101000010011001000100101001100100101
x_R = x – (d * (y * Math.Pow(2, -i))) = 0.984806574774655 Binary Values: 0.111111000001110001001000100111111000101011111100111
y_R = y + (d * (x * Math.Pow(2, -i))) = 0.173654859428127 Binary Values: 0.0010110001110100101001010001011000001001000010000110011
z – (d * angles[16]): -0.00126300742799264 – (-1 * 0.000874264213694023) = -0.000388743214298616 Binary Values: -0.000000000001100101111010000001110110010001010111001000001110001
d: -1
… Loop No:32
